lsp::least_squares< M, V > Class Template Reference
A functor for solving the Least Squares Problem. More...
#include <least_squares.h>
Public Types | |
| typedef M | matrix_type |
The type of the matrix object that represents 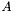 matrix. matrix. | |
| typedef V | vector_type |
The type of the vector object that represents 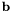 vector. vector. | |
| typedef matrix_type::value_type | matrix_value_type |
| typedef matrix_type::size_type | matrix_size_type |
| typedef vector_type::value_type | vector_value_type |
| typedef vector_type::size_type | vector_size_type |
| typedef matrix_value_type | value_type |
| typedef matrix_size_type | size_type |
|
typedef singular_decomposition < matrix_type > | singular_decomposition_type |
| The type of the functor object is used to perform SVD(Singular Value Decomposition). | |
Public Member Functions | |
| least_squares (matrix_type &matrix, vector_type &vector) | |
| An object constructor. | |
| template<class sV , class sM > | |
| void | solve (sV &ret, sM &cov) const |
| Solving operaton. | |
| template<class sV > | |
| void | solve (sV &ret) const |
Detailed Description
template<class M, class V>
class lsp::least_squares< M, V >
A functor for solving the Least Squares Problem.
The Least Squares Problem consists of finding vector 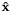 such that euclidean norm
such that euclidean norm 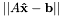 is minimal. Where matrix
is minimal. Where matrix 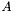 and vector
and vector 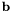 are given.
are given.
Constructor & Destructor Documentation
template<class M , class V >
| lsp::least_squares< M, V >::least_squares | ( | matrix_type & | matrix, | |
| vector_type & | vector | |||
| ) | [inline] |
An object constructor.
- Parameters:
-
[in,out] matrix The given matrix 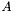
[in,out] vector The given vector 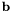
Member Function Documentation
template<class M , class V >
template<class sV , class sM >
| void lsp::least_squares< M, V >::solve | ( | sV & | ret, | |
| sM & | cov | |||
| ) | const [inline] |
Solving operaton.
- Parameters:
-
[out] ret Desired vector 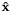
[out] cov The covariation matrix of the 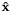
References lsp::singular_decomposition< T >::apply().
The documentation for this class was generated from the following file:
