lsp::singular_decomposition< T > Class Template Reference

A functor for the singular value decomposition (SVD). More...

#include <singular_decomposition.h>

List of all members.

Public Types

typedef T matrix_type
 The type of the matrix object to be decomposited.
typedef matrix_type::value_type value_type
 The type of the elements stored in the matrix_type.
typedef matrix_type::size_type size_type
 The type for seeking in the matrix object.
typedef banded_adaptor
< matrix_type > 		banded_adaptor_type
 The type of banded adaptor.
typedef bidiagonal_transform
< matrix_type > 		bidiagonal_transform_type
 The type of a functor for bidiagonal transformation.
typedef qr_decomposition
< banded_adaptor_type > 		qr_decomposition_type
 The type of a functor for QR decomposition.

Public Member Functions

 singular_decomposition (matrix_type &matrix)
 An object constructor.
template<class M1 , class M2 >
void apply (M1 &left, M2 &right) const
 Decomposition operaton.

Detailed Description

template<class T>
class lsp::singular_decomposition< T >

A functor for the singular value decomposition (SVD).

SVD is a factorization of matrix that

\[ Q A H = S \quad \mbox{where} \quad S = \left| \begin{array}{ccccc} s_1 & & & & \\ & s_2 & & & \\ & &\ddots & & \\ & & &s_{n-1}& \\ & & & & s_n \\ \end{array} \right|,\quad A \quad \mbox{is initial matrix,} \quad U, V \quad \mbox{are unitary matrixes,} \quad s_1 \ge s_2 \ge \dots \ge s_{n-1} \ge s_{n} \ge 0 \]

More widely known form of SVD is 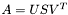$ A = U S V^T $ and this way there are obvious equations: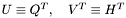 $ U \equiv Q^T,\quad V^T \equiv H^T $

Constructor & Destructor Documentation

template<class T>
lsp::singular_decomposition< T >::singular_decomposition ( matrix_type &  matrix  )  [inline]

An object constructor.

Parameters:
[in,out] matrix The reference to matrix object to be decomposited
Actual decomposition will be performed as soon as apply(M1& left, M2& right) will be called.

Member Function Documentation

template<class T>
template<class M1 , class M2 >
void lsp::singular_decomposition< T >::apply ( M1 &  left,
M2 &  right 
) const [inline]

Decomposition operaton.

Parameters:
[out] left The left matrix
[out] right The right matrix
The routine decomposites the matrix. Intrinsic assumption is that the all matrix are size-suitable.

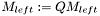
$ M_{left} := Q M_{left} $

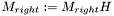
$ M_{right} := M_{right} H $

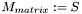
$ M_{matrix} := S $

Referenced by lsp::least_squares< M, V >::solve().

The documentation for this class was generated from the following file:
doxygen