lsp::givens_rotation< T > Class Template Reference

A functor for the Givens rotation transformation. More...

#include <givens_rotation.h>

List of all members.

Public Types

typedef T value_type
 The type of the elements used for constructing the transformation. 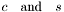$ c \quad \mbox{and} \quad s $ also have the same type.

Public Member Functions

 givens_rotation (value_type &x, value_type &y)
 An object constructor.
template<class U >
void apply (U &x, U &y) const
 Transformation operaton.
template<class M >
void apply (matrix_row< M > x, matrix_row< M > y) const
template<class M >
void apply (matrix_column< M > x, matrix_column< M > y) const
const value_type c () const
const value_type s () const

Detailed Description

template<class T>
class lsp::givens_rotation< T >

A functor for the Givens rotation transformation.

Givens 2d-rotation is a transformation defined as

\[ R \equiv \left|\begin{array}{cc} c & s \\ -s & c \\ \end{array}\right|,\quad \mbox{where} \quad c^2 + s^2 = 1 \]

For any vector 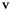${\bf v}$ given in advance there are 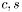$ c, s $ such that

\[ \left|\begin{array}{cc} c & s \\ -s & c \\ \end{array}\right| {\bf v} = \left(\begin{array}{c} \sqrt{ v_{1} ^ 2 + v_{2} ^ 2} \\ 0 \end{array}\right) \]

Constructor & Destructor Documentation

template<class T >
lsp::givens_rotation< T >::givens_rotation ( value_type &  x,
value_type &  y 
) [inline]

An object constructor.

Parameters:
[in,out] x The first vector coordinate. After construction 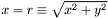$ x = r \equiv \sqrt{x^2+y^2} $
[in,out] y The second vector cooridnate. After construction 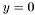$ y = 0 $
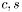It computes $ c, s $ such that

\[ \left|\begin{array}{cc} c & s \\ -s & c \\ \end{array}\right| {\bf v} = \left(\begin{array}{c} \sqrt{ x ^ 2 + y ^ 2} \equiv r \\ 0 \end{array}\right) \mbox{ for } {\bf v} = \left(\begin{array}{c} x \\ y \end{array}\right) \]

Member Function Documentation

template<class T >
template<class U >
void lsp::givens_rotation< T >::apply ( U &  x,
U &  y 
) const [inline]

Transformation operaton.

Parameters:
[in,out] x The first coordinate of vector
[in,out] y The second coordinate of vector
It computes

\[ \left|\begin{array}{cc} c & s \\ -s & c \end{array}\right| \left( \begin{array}{c} x \\ y \end{array}\right) = \left( \begin{array}{c} c x + s y \\ - s x + c y \end{array}\right) \]

and stores it in the x and y accordingly.

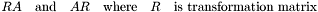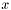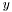Matrix operations, like $ R A \quad \mbox{and} \quad A R \quad \mbox{where} \quad R \quad \mbox{is transformation matrix}$ may be also computed if we represent the matrix as vector of vector-row or vector-column accordingly. Put it in other way we may assume that $ x $ and $ y $ are not scalar but vector values.

template<class T >
const value_type lsp::givens_rotation< T >::c (  )  const [inline]

Returns:
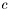$ c $ value is described above

template<class T >
const value_type lsp::givens_rotation< T >::s (  )  const [inline]

Returns:
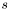$ s $ value is described above

The documentation for this class was generated from the following file:
doxygen